スポンサードリンク
|
|
リアルな世界で塾なしは本当に稀です。小学校卒業の時に塾なしなら、もはや天然記念物。
小学生から塾ありきです。
末っ子が現在小4です。
どこの塾に行ってるの?と塾ありきで話題を振られるようです。
兄の4年前より早期塾通いが着実に進んでます。
もう既に小4で天然記念物かも。
今では、低学年から塾産業はウェルカム♪
少子高齢化。早いうちから塾に飛びつくようなお客様はビジネスとしても美味しいのでしょう。
さて、最近の塾事情が分かってきましたので、この辺で書いておきたいと思います。
タイトル通り、
面倒見のいい塾が大人気です。
主に中学生の塾事情についての内容となってます。
どんだけ面倒見がよければ満足するのか?
中2からご縁があり某T塾に行ってますが、高校受験はノータッチ。
せっせと通って高校数学を進め、定期テスト前は受講をストップして、その時間を定期テスト勉強にあてる。
これを1年間繰り返してきました。
中二病に罹りましたが、高校数学だけは何とか腐らず先を行くことが出来ました。
後半は少しずつ回復し、自習室で定期テスト勉強をしてくることもできるようになりました。
某T塾がしてくれたことは、以下の通りです。
・某T塾がどれだけ素晴らしいか洗脳すること
・大学受験の厳しさを教える
・模試の分析と今後の大雑把な計画
十分です。本当に有難いです。
お陰様で、私も某T塾の虜になりました(苦笑)。
(カモにならないよう気をつけます。)
こんな感じですので、あまり管理されるようなこともなく、一応ノルマだけは気にしつつ自分で頑張ってきたと言っていいでしょう。
さて、こんな子は冒頭でも書いた通り少数派です。
タイトル通り、面倒見のいい塾が大人気です。
多分、私達が知ってる塾とは別物だと思った方がいいです。
| 1. |
過去問を配る
個人面談の時、学校の担任の先生にも聞いてみたら困惑されてました。 近隣の塾に過去問集があるから、先生も新しい問題を作るの大変だと思いますが、重箱の隅を突くような問題を出すのやめて〜 ここまでは中学入学までに想定していた範囲内です。 |
| 2. |
学校のワークを塾がチェックする。
うちは、学校から指定された提出日が期限です。 これを知った時、俺も塾で管理してほしいと訴えてきました。 |
| 3. |
学校毎に予想問題を塾の先生が作ってくれる。
過去問を配って終了じゃないんですね。 雑談部屋にも少し書きましたが、愚息は仕方がないので1教科だけでしたが、自分で作り先生に見せに行ってます。 |
| 4. |
予想問題の出来具合を元に定期テストまでの計画を塾が立ててくれる。
定期テストで点取るために、塾が全力でサポートしてくれます。 勉強を教えるだけではなく、勉強の基本的なやり方を教えるだけではなく、手取足取り教えてくれます。 あまり聞いてませんが、もしかしたら学校で配られる定期テスト計画表も塾がチェックしているかもしれませんね。。。 |
このように、面倒見がいい塾が大人気です。
私立中高でも、面倒見がいい学校が人気のようですね。
面倒見がいいと、そのまま言われたことを消化していけば、点数が取れるから?合格するから?
親子で余計な遠回りはせず、一直線を好む。
理由はこれ。
・余計な苦労・失敗はさせたくない。安全な道がいい。ラクに点取って合格できた方がいい。
・親子バトルは極力避けたい。
・家庭学習の工夫?そんなものより手っ取り早い塾のノウハウ(面倒見のいい塾)の方が確実である。
・正面突破より、さっさと推薦で入試を終わらせた方がいい。
もう挙げたらキリがない。
とにかく我が子をぬるま湯につけておきたいのが親心。
これが面倒見のいい塾が大人気な理由なのかもしれません。
大学受験は膨大な量をこなさないといけないため、現役合格するには効率の良さも求められます。
そのための塾利用も一理ありますが、またまた課金しまくって全教科を塾に教えてもらうつもりでしょうか。
うちですか?
最初聞いたとき、T大卒夫も私もビックリしました。
・どんだけ受け身の姿勢なんだ
・自分で試行錯誤して自分の勉強スタイルを確立していく時期
・社会人になって試行錯誤の時期はない。試行錯誤は今の時期だけ。
・大学受験も塾漬けでいくつもりか
・与えられたものだけを消化していくことに疑問を感じないのか
・自発的に学ぶ姿勢がなければ、どこかで躓く
ざっとこんなことを子供たちに説明しました。
塾は合格するまでのお付き合いです。
もし塾通いを考えているなら、目先のことだけじゃなく、もっと先のことも考えた上で指導してくれる塾を探してみてください。
面倒見のいい塾が大人気なんてどうかしてます。

余談です。
写真のお肉は左から、
鹿(ジビエ)、ラム、豚、鶏、牛です。
牛だけでいいと言いましたが、肉の食べ比べをしたいとT大卒夫が言い張るので家族で付き合いました。
あの懐かしいクレイジージャーニー(片桐さんの回)を思い出しながらの実食。
鹿肉は低カロリー高たんぱく質そのものでした。次は猪にしたいそうです。。。
総論
綺麗ごとのように聞こえますが、目先のことより、もっと先のことを考えたら、何もできない子に育ってしまうと思いませんか。
ガッツリ干渉したい気持ちは当然あります。失敗を回避できるので。でも、これをやってしまったらアウトだと思ってます。
最初から出来る子はいません。
自分でどうしたらいいのか考えてやっていく。
そんな試行錯誤をしていくうちに、自分に合う効率の良いやり方を見つけていくのではないでしょうか。
点とらなきゃ、内申とらなきゃ。合格しなきゃスタート地点に立てないじゃん。
そんなの綺麗ごとだと思う方もいるかもしれません。
その通りです。
でも、人生のゴールは合格じゃないですよね。
本物の教育、与えたいと思いませんか。
最後に丁度タイミングよくこの議題に核心を突くコメントが届きましたので、ご紹介してまとめとします。
何かを狙って外から与えること以上に、子ども本人が自分の中で探し当てることによって上達につながるといいますか。
そこにしか学びの本質はない気がしています。
痺れました。
私からは、何もいうことがありません。おっしゃる通りです。
 Copyright secured by Digiprove © 2021
Copyright secured by Digiprove © 2021スポンサードリンク





長すぎるコメント、大変失礼しました。
私自身中学から私立だったので、高校受験のために内申をあげることが重要だということをみなさんに教えていただくまでよく分かっていませんでした。
少しでも内申アップのお手伝いになれば、と思い、田舎の某私立中学の一例として書いてみました。
ふふふさま
私自身も凸凹なので、放っておいても息子は凸凹になりつつあり・・・こういう子は成績では評価されにくいですね。
でもふふふさまのところは上位校におられるのだからすごい!
肯定ペンギンさま
いつもレスくださってましたよね、改めてありがとうございます。
新小2のこと、色々お話ししたいですね〜!
この間最レベ一年買っちゃいました!
これで一年生の問題集は打ち止めにしたいです。
詩人の母さん コメントありがとうございます。
内申話、ありがとうございます。
前髪には笑ってしまいましたが。
こちらももう少しで内申が出ますので、またコメントさせてください。
最レべ1年。頑張ってくださいね。
我が家は最低でもこのレベルだと思ってやっていってます。
返信すると一つ段落が下がる件についてです。
iPhoneを横にすると、PCと同じように返信したコメントについては段落が下がって表示されます。iPhoneユーザーの皆様お試しください。
横!
androidユーザーですが、段落がずれて行ってました。縦の方が読みやすいという思い込みのワナでした。ありがとうございました。
ところで、かわいそうなゾウ様
以前知らなかったとはいえ、「家に先生がいてうらやましい」と軽々しく言ってしまってすみません。「先生の子」というのは重圧ですよね。それを思いやる親心を知らずに一般論を言って恥ずかしいです。お子様の好成績は、そういった親心に応えていらっしゃるんだと思います。立派です。これからも親子で駆け上ってください。ずっと気になっていたので、コメントさせてください。
詩人の母様
うちはハイレベ1年で悪戦苦闘しています(汗)。文章題以降は夏休みの予定。最レべは無理そうです。小2では最レべに挑戦できるぐらいに頑張りたいと思います。まずはコツコツ教科書ワーク。
肯定ペンギン様
とんでもありません、以前のコメントでペンギン様の言葉に大変勇気づけられました。お気遣いありがとうございます。「先生の子」という重圧は、確かにあります。田舎は親の職業も筒抜けなので…。でもここで皆様にコメントをいただいて、今はしっかりサポートして娘と二人三脚でやって行こうと改めて思えました。ありがとうございます。
Androidでも、画面を横にすると段落が下がりますよ〜
皆さん コメントありがとうございます。
>朝と夜の1日2回、投稿は1日1回、中毒性が高い
すみません、笑ってしまいました。守られてない方大多数(笑)。
結構際どいことを皆さん書かれるので、中毒性が高いとおっしゃる気持ちは分かります。
頻発して登場する方々は、頭の回転がいいんですよね。
あの展開の早さに、殆どの方が書くところまでもっていけないはず。
私も交通整備出来ているのか、非常に怪しいですので。
失礼のないようにやっていきたいのですが、どこかで漏れがありそうで。。。
質問されているのに、吹っ飛ばしてしまっているとか。
そこだけが気になるぐらいです(汗)。
内申の話ですが、おふさんと詩人の母さんがせっかく書かれているので、内申が出たらご報告します。
最低42は欲しいです。
足りてるといいな。。。
でもあいつだからな。。。
私立中高の話は面白かったです。
総合型選抜の割合がこれからも増えていくことを考えると、高校の定期テスト・その他の諸々が大事になってくるかと思っています。
実際、某T塾でも、まずは学校。学校の評定が大事です。
複合型、前期と2チャンスと思ってくださいと言われましたので。
私立にいこうが、公立にいこうが、結局は内申が付きまとうのでしょうね。
Zさんのコメントにまたハテナが。
授業だけで100点ズラリだったら、先生の教え方が上手ってことで◎ズラリな気がするのですが。。。
うちの子達は塾なしだと分かってるので、いつも凄い凄いと言われます。
塾行ってることが前提で話が進んだ時は愕然としましたが。。。
コメント欄と評価が一致しない。
本当、謎ですわ。
うちは、あまりそのような矛盾がない気がします。
〇と◎の話があちこちで頻発していて、どこに書こうか迷っているうちに2日経過してしまいました。
流れ的にやっぱりここのほうがしっくりくるので、忘れないうちに書いておこうと思います。
息子も〇ばっかりだったので希望的観測ですが、基本的に
〇求められるレベルに達している。
△達していない。
の二つしかないのだと思います。
なので100点ずらりなのにどうして〇なの?って思われるかもしれませんが、
〇=5段階の3とか4、ではないのだと思います。
だって〇と△しかないんだもの。
できているかできていないのどちらかなのでしょう。
◎は・・・他人には見えない先生のボーナススイッチを押してしまった時につくのだと思います。
このブログで時折ミニ先生のことが話題になりますが、
先生に言われるからイヤイヤやっているのか、自分で教え方を創意工夫してやっているのか、
これも〇と◎の分かれ目だと思います。
また「授業中によく発言して~」というのもくせものですよね。
授業の流れと関係なく先生の説明を遮って質問したり「はい!はい!」と手を挙げても、
ただの授業妨害と受け取る先生もおられるでしょうし、他人と同じ発言や質問を繰り返していると
「この子は他人の話を聞いてないな。」という無駄に低い評価を受けることにもなりかねません。
別の記事のコメントで、◎の数は地域や教師によってずいぶん差があるようですし、
低学年のうちは◎はオマケ、それよりも△がついたら要注意、ぐらいのつもりでいいかなぁ、なんて思っています。
でももう少し◎がほしかったな・・・。(ぼそっ)
投稿は1日に1回にしようと心に決めていたのに、早速破ってしまった詩人の母でした。
詩人の母さん 何度も?コメントありがとうございます。
ボーナススイッチは置いといて、、、(笑)、
ミニ先生や発言に関しては、その通りだと思います。
思い出した!!
どこかで書いたかもしれませんが、うちの小学校は△がついてなければ喜んでくださいみたいなことを言われました。
管理人さんいつもありがとうございます。
私も思い出しました!あまりにも◎が少ないので1学期の時に確認したらほとんどの子が◎はついてないと思ってください。
◎があるということはとても出来ているの意味です。と言われました。
でもよくよく考えたらそんなことあります?なんと厳しい学校と思ったのを思い出しました〰。値打ちこきすぎでしょ。
通知表の格差はA評価、B評価の違いです。できたらAなのかBなのかの違いです。つまり、A評価の学校は高くなり、できたらB評価であれば、Aはなかなかつきません。87点でしたら、A評価の学校であればA、B評価の学校ではBになります。B評価の学校では100点近くではないとAにはなりません。ちなみにうちの子の学校はA評価、隣町はB評価で学校の方針によって変わります。市内でも統一されていません。今は、B評価が主流だと思います。昔はA評価が主流です。
RHMさん
なるほど。とても納得できました。
わかりやすく教えてくださりありがとうございました♪
貴重な◎沢山褒めてやろうと思います(╹◡╹)
塾に入れるか入れないかは、親御さんが自信あるかないかだと考えています。親自身が高学歴だったり、塾なしでなんとかなってしまったら、あまり熱が上がりませんが、親が学歴に自信がなかったり、旦那さんの稼ぎがよかったりすると、異常にヒートアップします。私自身の経験上、道内トップ高で、トップ入学した友人は北大落ちてます。中学時代天才でも燃え尽きている人、勉強ばかりしてコミュニケーションが取れなかった人、高校ではじけてしまった人・・・いろいろいますよね。高校は通過点なので、そこで底上げし過ぎると後が続きません。お金も能力も。小六の時点でもう順位はついていて、今年もほぼ予想通りの合格状況。蛙の子は蛙。
RHMさん コメントありがとうございます。
すみません。見間違えだったらすみません。
確か教師ですよね。
いいですよ。ここではガンガン書いていただいて大丈夫です。
嵐が来ましたら、何とか交通整備しますので。
>そこで底上げし過ぎると後が続きません。お金も能力も。
まあ、ハッキリ言えることは、どこの家もお金持ちに見えますね。
お金と能力の話は、リクエストが以前ありましたので、どこかで更新したいと思います。
>小六の時点でもう順位はついていて、今年もほぼ予想通りの合格状況。
まだ分かってない子もいますが、そのうち風の便りで分かるでしょう。
学校レベルが到達していない集団でミラクルが起きることはなかったようです。
この辺は、歓談部屋でこんにちは。さんがトップ層以外は大したことがないと冷静に分析されてます。
皆さん コメントありがとうございます。
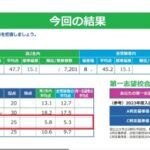
雑談部屋で書きましたが、内申は最低ラインに一つ足りませんでした。
まあ、中二病が響いたということです。
あいつは凄い。
先生捕まえて、何が悪かったのか聞いてきたようです。
3はありません。4と5だけです。
今回の結果は納得しているようです。
3年生は絶対に頑張ると言ってますが、本当に気が抜けないということだけは分かりました。
いつも色々と教えてもらっている方の中に新中1生の方もいらっしゃるので、先にコメントで書いておきますね。
定期的に出すレポート。AとBが混ざってると、5はもらえないよ。
音楽鑑賞、美術鑑賞、興味のないものでも、頑張って書く。
何がいいのかさっぱり分からないなんて芸術音痴なことを言ってる場合じゃないです。
愚息はBが混ざっていたっぽいです。
今回オール5に近い子がいたようです。1つだけ落としたぐらいだったかな。
愚息より断然上です。その子自身も驚き、つい周りに言ってしまったのかもしれません。
「〇〇が発言したところ、見たことがない」
はあ?あなた居眠りしてるんじゃないの?と言いたかったのですが、やめました。
彼の授業中の態度はどの教科も全てAですので(笑)。
謎です。
てっきりおふさんが書かれている「人前で発表する力がない子」はどんだけ点数を取っても4だと思ってましたので。
今度、内申についても更新しようと思いましたが、ちょっと自信がなくなりました。
詩人の母さんとおふさんが書かれているあざとい女子なのか?
匿名1さんが書かれているように、授業態度はほぼ見てないのか?高校受験組でそれはないとは思うのですが。。。
盲点だったようで、ちょっと信じられないとまで発言しています。
このような子が、世の中上手く渡っていくのかもしれませんね。
少しは見習ってほしいです。
ネクストコービーさん。
遅くなりました。
用意されたプリントに食いつかず、自分の不出来を自分で分析して補う。
大事ですよね。確かに、息子くんの言う通り、効率がいいんだと思います。
小さいうちは、親と二人三脚でやっていくのですが、そのうち一人で責任もって取り組むようにしないといけないのかなと感じています。
問題集1冊選ぶのにも、自分で選ぶ。
実際は、まだ親からのアドバイスも必要ですが、社会の問題集は自分で選んできたので、そんなことが少しずつでも増えていけばいいのかなと思います。
結局、こんなことの経験が、大学受験やその先の社会に出た時、受け身ではない責任のある姿勢がみられるのかなと。
私もたまたまテレビをつけていて、多分同じ番組だと思いますが、見ました!
同じく興味深かったです。
もし、もしもですよ、東大に入れてベンチャー就職となったら、親はどう反応したらいいのか。
いや、もう立派な大人です。
親が、「失敗したらどうするんだ。安定が一番だ。」なんて言ったらよろしくないのでしょうね。
見ていて、私は背中を押せるかしら。と不安になりました。
ありがとうございます。
通知表のことです。
参考にはならないと思いますが、小テストは多分満点、提出物の評価はうちの学校は教科によりあり、なしがあります。
音楽はあったようで、多分Aだったのだろうと思います。
今年はコロナだったので、鑑賞が多かったはずで、ピアノを習っていることもあるのか小学生のころから知識は豊富なので有利だったはずです。
美術も昔から絵や工芸品が好きで小学校のときから美術館、博物館通いをし、読書はしない子なのですが美術本だけは読んでいたので知識は同年代の子より豊富だとは思います。
あと発言についてですが愚息に話を聞いたところ、自分から発言するシチュエーションがほぼないようです。
先生からランダムに当てて答える形だそうです。
ここで答えられないと減点になるのかもしれません。
今まで答えられなかったことはないようです。授業を聞いていれば答えられるものだそうです。
今回ほぼオール5と書きましたが全てが5ではありません。
酷語、捨会は5でしたが、退育は5ではありません。
そもそも退育が5を取れるとは考えたこともなく、小さいときから親の目から見てもすきなんだろうけど、イマイチだと思っていました。
私は何もしなくても退育は得意だったので何でできないのか疑問で小さいときは公園に連れ出してバトミントンをさせたり、ボール投げをしたりしましたが結果は今ひとつ。
習い事も続かず。
あきらめて途中でさじを投げました。
やってもどうしようもないものはどうしようもない。
体育ができず、音楽、美術が得意な男子は中学ではモテないようです。
顔だけじゃだめなのよ。
体育ができないと男として認められません。
匿名1さん コメントありがとうございます。
なんちゃら鑑賞は確かにコロナと関係してそうです。
歌・リコーダーは学校再開しても出来る状況じゃなかったと思います。
うちは、ご存じの通り体育会系一家なので、博物館・美術館はあまり縁がありませんでした。
連れて行ったこともあるんですよ。
高い入場料を払って素通り。同じく諦めました。
まあ、仕方がないです。
自分で何とかしてもらうしかありませんよね。
運動とモテ度の関係ですが、良友も悪友もスポーツは出来てモテるようです。
今の子達、中学生でも普通に付き合っちゃいますからね。。。
息子くん、そういえば中学に入っても浮かれた話がないですね。
モテない方がいいですよ。
今日も少し聞いたら、何で〇〇があんなに内申いいのかさっぱりわからないと言ってました(汗)。
こりゃ、内申制度が嫌われるのも無理ないです。
14・15の年齢で、世の中の理不尽なことを経験するのですから。
こんばんは。 春から公立高校2年の娘がいるぽっけです。
公立高校受験では内申、大事ですよね。学校によっても厳しかったり甘かったり…。
色々気を付けるポイントはみなさんが書かれているので、ちょっとしたことなのですが参考になれば…。
娘は3年間オール44でした。体育は苦手なので、ペーパーで頑張っても実技はBなので これが娘にとって最高の評価です。
ガツガツ内申を取りにいくようなタイプでもなく、先生と仲良くでる世渡り上手なタイプでもなく、むしろ先生としゃべるのは苦手な大人しい感じです。
発言もあてられれば答えるくらいです。(大体その日の出席番号から順番にあてられていたそうです)
ちょっとしたポイントですが、姿勢をよくする。
これだけです。すみません、大したことない情報で。。
でもよくほめられたそうです。
授業参観で娘を見た時も、背筋ピンとして先生をしっかり見て話を聞いていました。
それだけで一生懸命聞いている風(笑)に見えるんですよね~
頭の中で何考えててもいいので、誰でもできるちょっとしたポイントです(笑)
娘は内申のためではなく、ダイエットのためにお腹に力を入れていたそうです。女子ですね~
高校では、周りは勉強だけできる人ばかりじゃないんだよ、と言っています。
絵が上手な人も多いし、楽器が弾ける人、スポーツも得意、SNSに毎日作ったお弁当を載せている人、趣味も幅広く、多才な人が多いそうで、刺激を受けています。
五教科以外の内申が良いのも納得です。
娘も絵を描くのは好きですが、こんなレベルじゃなくて、もっと才能があることがあればなーなんて言っています。
勉強だけでもついていくのが大変なのになぁ。。
すみません、訂正です。
私の勘違いで出席番号であたるのは高校でした。中学は挙手制だったそうです。
確実にわかる問題には手を挙げていたよ、と言っていました。知らなかった…
姿勢の件、賛同してもらえて嬉しいです(*^^*)
管理人さん、お疲れ様です!
やはり内申は女子の方がとりやすいような気がします…(-。-;「優等生」な子が多いですから。授業中、積極的に発表しなくても、「5」とれるのですね!
うちの旦那もぽっけさんのところと同じく、体育以外5だったそうです。目立つタイプではないのですが、それでも要所要所は発言したと言っていました。
ちなみにぽっけさんのところが意識していた授業中の態度ですが、私も全く同じことを心がけていました。姿勢を正して、先生の方を向き、時々頷く。こうした授業態度も大切ですよね。
オール5に近かったその子は、定期テスト、小テスト、提出物のクオリティ、全てが5の基準に達していたのかもしれません。体育や音楽はその場で実技があると思うので、ごまかすことはできませんが、美術は家族総出で質の高いものを提出することもできます。(休暇中の課題のみですが)
それにしてもお兄ちゃんは、全て自力で頑張って偉いなと思います…親に頼らないタイプですよね。最終的にはそういう子が生き残りますよ。
姿勢!激しく同意です。
呼ばれた時に目を見て返事とか、こういうところに躾とか育ちの良さがでますね。
色んなことに興味をもつキラキラした瞳も好印象です。
発言しないのに内申がよかった子・・・これまでにコメントあったこと以外では、質問に行ってたのかもしれませんね。
内申を上げたい人は、聞くことなくてもテスト前に全教科の先生に質問に行く!ぐらいの意気込みが必要かもですね。
でも間違っても「テストは何が出ますか?」はダメですよ!
「私は授業聞いてませんでした」って授業態度を自ら下げに行くようなものですから。
その教科に関する雑談でもいいと思います。
テレビで見たことを話題にするとか。
これが「主体的なんとか」の評価につながるのかも。
質問に来た子は先生の記憶に残ります。
評価にも影響が出やすいと思います。
今年はコロナ禍でグループ学習も少なかったと思います。
日頃、管理人さんのお兄ちゃんはこういうところでリーダーシップを発揮したり面白い発表をして評価も高かったのでは?
接触を避けた、ひたすら講義型の授業では、元気な子は力を発揮しにくかったかもしれませんね。
ぽっけさん おふさん 詩人の母さん コメントありがとうございます。
うちの娘、姿勢がいいらしくて躾に厳しそうな担任の先生から褒められたことがあります。
きっとオール5に近い子は、姿勢もいいでしょうね。
私も詩人の母さん同様、納得です。
ぽっけさんの娘さんが感じている多才ですが、クラスでオール5に近かった子には全く興味がなかった(←笑)ようで、何が得意なのかすら分かってなさそうです。
クラスが3年でも一緒だったら、その辺も学べるんですけど。
気づくのが遅かった…。
先生へ質問しにいってるかどうかも分からず。でも、してそうだ。
>中学は挙手制
うちの中学も挙手制です。
挙手しているところを見たことがないと言ってます。
多才な話は、匿名1さんの息子くんが通ってる中学でもそのようですね。
勉強だけって子は、案外少ないのかも。
ぽっけさんの娘さん、44だったかあ。うちは3点足りず。
43ぐらいなら何とかなりそうですが、内申はあった方が絶対にいいので、目指したいです。
と言っても、親が出来ることが何もない。
夏休みなど、美術の課題もありましたが、自分でアイディアから仕上げまで一人でやってました。
納得いくものが出来たら、嬉しそうに見せてくれます。
以前、作品の話が話題になりましたが、うちはやっぱり手伝わないです。
だから、この結果なのかもしれませんが、手伝ってるところを主人に見られたら、激怒ものです。
聞かれたら答えるぐらいはいいようですが。
>最終的にはそういう子が生き残りますよ。
おふさん、そうだといいのですが。。。
おっしゃる通り、そんなところを意識しております。
でも、おふさんも生き残ってますよね(笑)。
低学年だと、親が楽しんじゃうって話もありましたが、ちょっとこれは考えられないです
逆に子供から、「これ、自分の作品じゃなくて親の作品だ」と言われないのかしら。
そこが凄くひっかかりました。
めばえや幼稚園の紙付録を作るとき、さっさと作り終えたくて、ちょっと私がやりやすいように触ろうとしたら、すっごく怒りました。
この辺は性格にもよるかもしれませんが。
おはようございます。
あぱねこです。
先日、あおいが佳作を取ったので、県の交通安全ポスターポスター入賞作品展示会に行ってきました。
そこに並ぶ作品を見て唖然としました。
どう考えても低学年でこのクォリティーはないでしょ?な作品がズラリでした。(ガチの大人作品(笑))
もちろん、子供がひとりで描いたと思われる作品もあります。不思議ですが、そういう作品の方が目を引きますね。
自分の力で一生懸命描いた子の作品は、素人が見ても分かるのに、、、。
どんなに不格好でもバランス悪くても、最初から最後まで自分でやり遂げる事に意味があって、そこを評価されるコンクールや内申であって欲しいなと思います。
「夏休みの宿題の工作を親が手伝って楽しかった記事を見た。」は私のコメントです。その時も書きませんでしたが、「提出必須の宿題をやる気がない低学年」の話でした。説明不足です。やる気がある子だと文句は出そうですね。親の関与は夏休みの工作を作品と取るか、体験(低学年です)と取るかにもよるのではないかと思います。提出が任意なら、親も助かるのですが。
うちは折り紙で「よく飛ぶ紙飛行機」を作って持っていきました。しょぼい。
私自身は、6月から学校が始まった小1の読書感想文が立派すぎるのが気になりました。公立しかない市の文集です。
私自身が姿勢が悪いので気を付けます(汗)。姿勢がいい子はきっと家庭の教育がいいのでしょうね^^
あぱねこちゃん 肯定ペンギンさん コメントありがとうございます。
あぱねこちゃん、入賞おめでとうございます。
入賞した作品を見に行くのは嬉しいですよね!うちは絵が3人とも凡レベルです。
そういえば、以前、スケッチの本を買って4人で描いた時がありました。
更新するって言っておきながら、もう2年?ぐらい経ってしまったかも。
私も子供3人いるので、一応経験があります。
学校で作ったので、何を作ったのか全く知らず。皆さん、言っておきますが、私の手は一切はいってませんので(汗)。
それにしても、何で学校は親の作品を選んじゃうんでしょうかね。
100%分かってるはずなんですけど。
自由応募だと、数が少ないから選ぶしかないとか。
作文は卒業文集の時に真面目に取り組んだかどうかバレます。
と言っても、こちらも家に帰って親からヒントを得られたら書けちゃうのですが。。。
とある方のお子さんのように、物語を作るのが好きで原稿用紙100枚書け~とまでは言いませんが、下手でもいいので自分で1から考えて作り上げていく経験は大事だと思います。
最初は真似でもいいんですよ。
そこから、上手くなっていけばいいんだと思います。
リアルな話でも、低学年で読書感想文に選ばれた話は聞きます。
1.構成や内容など全部自分で考え、親はまともに読めるよう整えただけなのか?
2.どの本で書くのか?から全て親と一緒に書いたのか?
低学年の場合、100%親が手を加えることなく提出することは無理だと思ってます。
どこまで介入するか?
ここでしょうね。
〇年連続入賞、今年は本人がやる気なしと提出すらしなかった親子は間違いなく1.でしょう(笑)。
肯定ペンギンさん。
やる気のない子の親が作品を作っちゃう話だったのですね。
教えてくださりありがとうございます。
よく飛ぶ飛行機は自主勉で娘がやってましたが、なかなか難しいらしいです。
管理人様や他の方のコメントを見るまで、高学年で親の関与がそこまであると思っていませんでした。
私自身の親の関与は、低学年は覚えていないのであったのかも知れません。高学年では、夏休の計画表の天気の部分をさぼって、夏休みの最後に親と「雨はいつだっけ?」と言いながら埋めたぐらいです。休み明けだけ工作がうまくなる子もいなかったです。選ばれる子は普段から上手でした。時代が変わったんですかね…。
交通安全ポスター募集のカラーのチラシを見ましたが、選ばれているのは背景までちゃんと仕上げている作品でした。うちの子は背景は真っ白なので応募できません。
絵画を習っていなくても、風景をきちんと捉える子はいるみたいです。子供の友達が描いてくれた似顔絵を見たら、上手ではないけれどもちゃんと特徴をとらえていて、そんな子は背景もきちんと描けるようです。
「清水義範の作文教室」を読んでいますが、作文教室に通っている子でも、それほど立派な文章は書けません。でも読書感想文集に選ばれる子の文より面白いのは確かです。
よく飛ぶ飛行機は「なんちゃって」で、コクピットにウサギを描いてましたよ…。
肯定ペンギンさん コメントありがとうございます。
今の親は、育児も丁寧なんだけど、過保護気味な気はします。
親の言う通りに動いていれば大丈夫。
歓談部屋でも、田舎県トップの入学式で上記のようなことを言われたと、とあるお父さん(←笑)が書かれていましたが、本当にそのような子が多いんだと思います。
失敗させないんですよ。
子供に考えさせたら、経験がないですから失敗しますもんね。
だから、考えさせる機会を与えない、丁寧な塾も繁盛するんだと思います。
ちなみに、私も主人から、成長の機会を奪うな~と叱られます。
清水義範の作文教室、面白いですよね。
コメント欄で日本語必笑講座が面白いと紹介があったので、こちらも読みました。
鋭いツッコミに、感心しながら読みました。
サラさん、ご紹介ありがとうございます。
管理人様
日本語必笑講座、いい本を教えていただきありがとうございます。表紙が秀逸です。古い本ですが、中島らもさんの、関西の看板コレクションもおもしろいです。「西方冗土」だったと思います。(検索しても出てきませんでした。)
春休みの算数テコ入れに失敗し、特性のある子に対応した「すらら」という教材を検討中です。計算間違いを連発し、ちょっと難しい文章題は読もうとしません。算数に対する拒否反応がひどくて、本人がやる気になるまで放置も考えたのですが、今取り残されると本人が苦労をするのが目に見えているので「すらら」を試してみて、ダメなら学習障害の診断を受けるかも知れません。学習障害の懸念がなければゴリゴリ行くのですが。くもんも頭をよぎりました。溺れる者は藁をも掴む感じです。このスレの趣旨に反してますが、不安で不安でたまりません。
ハイレべ算数1年は、子供に任せてできる問題だけやらせたのですが、中級ぐらいの問題が出来たりもしたので、何が正解か分からなくなりました。最後の方は慣れてきて、自分の苦手分野だけ的確に飛ばしていたので、全くできない訳でもないんです…。かなり飛ばしてましたけど^^;誰にも話せないので愚痴ってしまいました。すみません。
おはようございます。
肯定ペンギンさん
娘さんが、算数に対して拒否反応が激しくなってしまった件を
読ませていただきました。
そんな場合「算数ラボ」が非常にお勧めですよ。
なんと言っても問題が1ページに1問のみ!のところで抵抗感が薄れると思いますし、余白もたっぷりで、絵もあり見て解いて楽しい構成になっています(^^)
レベルも10級からありますので、娘さんに合った級から始める事が出来ると
思います。
管理人さんのブログでも、度々話題になっていますよね。
息子は算数ラボは大好きで、今も時々気分転換に7級をしています。
息子も1年生の時、文章題をキチンと読まずに数字のみを拾って勝手に計算する…といった感じだったのと、文章題に抵抗感が激しかった事から算数ラボを始めました。内容が楽しいので、遊び感覚で出来るかもしれません。
受験塾で模試を受けている中、最後には算数ラボで出題されてた思考力系の
問題が必ず出題されます。知らずにやらせていましたが「やってて良かった!」と
思いました。1度試されてみてはどうでしょうか(^ ^)
こんにちは。
算数ラボについての訂正です。
1ページに1問のみ!と書きましたが、2〜3問のページもあります。
失礼しました(^^;
我が家は「算数ラボ」のみで、「算数ラボ•図形」はしていません。
ただ、通常の算数ラボでも図形は出てきます。
お子さんとの相性もありますが、ゲーム感覚で出来る楽しいドリル
です^ ^
まりお様
温かいコメントをありがとうございました。算数が得意と思っていたお子様に、そんな時期があったとは意外でした。
この一年、市販教材を色々試してみてどこにも当てはまらず、それより下となったら外注するしかないか思い始めていました。
計算はくもんの「1+1,2+1…」が続くドリルを最初にやって、余りの機械学習に子供が拒否反応を示し、できるが増えるドリルあたりをウロウロしていました。文章題は今も単純なものでもミスをします。でもそれが特性なら、理解できない子供に酷いことをしていたのではないかと新学年を前に途方に暮れていました。
算数ラボは、検定用の難しい教材だと思っていました。まだ踏ん張る余地はありそうです。。うちの目標は学校で100点を取ることです。子供と一緒に頑張ってみます^^
こんにちは。
肯定ペンギンさん
我が家も1年生の時は色々ありました(汗)
なんせ、入学して早々ずっと両手を使って計算を
してましたから。。。
「計算に慣れて来たら、指を使うのが面倒になって
自然とやめるかな?」
と思って見守っていたら、まずい事に指を使う事が当然となり、逆に定着してしまってました。
それを無くす為に、夏休みに指を使えない様指を押さえながら(鬼母)百マス計算のトレーニングをし、なんとか頭で計算が出来るようにはなったものの、今度は文章題を読まずに数字のみを拾って計算し間違える。。。
こんな感じです(^^;;
そして、1年生の後半で掛け算の練習をした時、足し算を間違えまくるという混乱が発生!足し算を改めて覚え直す。とかもありました。
国語中心で家庭学習を進めていたので、あまり算数に時間を割けず、1年生の時は何だかバタバタで終わってました。。。
そう言えば…1年生の春休みには、水色の表紙の
「田中先生の算数絵解き文章題」もやってました。
絵を見ながらや、自分で絵を描いて文章題を解くドリルです。息子は絵を描くのが大好きなので、抵抗なく出来ました。割り算はやらずに、無理のない範囲で楽しんでやってましたよ。内容は、あまり難しくないです。こちらもお勧めです♪
子供の教育については、未だに悩みが尽きませんが…
一緒に頑張りましょうね(^^)
我が家は昨年夏頃、学校であまりにも単純計算の学習が続いて親子共々参ってしまい、算数ラボに逃げていました。
どんぐり倶楽部という怪しげな(失礼!)ものにも手を出していました。
肯定ペンギンさまのお子さんは多読、とのこと。
どんぐり〜はハマると楽しいかも。
うちの息子も(←と、肯定ペンギンさまのお子さんと一緒にしてしまいましたが)空想ワールド爆発な人なので、それはそれはすごい世界観が繰り広げられていました。
ある時はたと「これって算数の問題?」と気付いてしまい、熱が冷めたみたいです。
うちはそこでストップしました。
算数ラボも9級に入った時点で「これやめる」と言ったのでストップ。
ラボもどんぐりも必須のものではないので、今後はよっぽどやりたがらない限りはやらないと思うなあ。
でも、今振り返るとあの時には必要なものだったのかも。
どんぐり〜は親の忍耐力が試されるように思います。
まりおさま、詩人の母さま
お子様のことをお話しいただきありがとうございます。色々なことを試してこられたのですね。
うちは年長後半におはじきや百玉そろばんを使って数量問題を教え始めたのですが、全く理解できていないようでした。おはじき・百玉自体が恰好悪いらしく、拒否でした。日常生活で使う数量はわかっていましたし、ちえあそびはやっていましたので、1年生で習う頃には成長しているかと先取もせず、教科書通りに進めました。それがこの有様。
まりおさまのお話を聞いて、似ている点がいくつかありました。不安なのか、秋まで見直しの時に指を使ってました。学校で言われたのか冬には使わなくなりました。かけ算もあるあるです。勝手に友達のマネをして始めて、またちょうどそのころに復習で繰り上がりのない計算ばかりしていたら、繰り上がりができなくなったりしてました(驚。)
文章題のやりはじめに使っていた「4コマで考える算数文章題」という超簡単なのも理解できていないようでした。足すか引くかわからない感じで…。サイパーでようやく、絵を見て解きだしましたが、図を描くことはできてません。
どんぐりは例題を見たことがあります。文章は複雑ですけどユーモアがありますね。一度試してみます。算数の問題と気づいてやめるお子さんに思わず笑ってしまいました。うちは文章そのものに興味がないと読まないみたいなので、う〇〇ドリルとかなら読むような気もします。う〇〇の文章題問題集があればいいんですが。「絵解き問題集」はすごくよさそうですね。調べたらもう新品は売っていないみたいです。残念です。
このサイトでこのようなお話が聞けるとは思っておらず、コメントしたときは絶望していました。もう少しできることを頑張ってみます。好きなことは嬉々として取り組んでいて楽しそうなんですけど、算数ができないと今後苦労するの心配です…。
肯定ペンギンさま
昨日本屋でチェックしたらう○○ドリルの一年の総復習ドリルには文章題ありましたよ!
取り急ぎご報告まで
森羅さま
ひとりで学べる算数、内容は魅力的でしたがボリュームがすごいので今年は教科書ワークで頑張ります。来年はひとりで学べるにする予定です。
詩人の母さま
復習ドリルまでは見ていませんでした。早速チェックします♪
どんぐり、面白いですね。例題を試してみます。お絵描きで終わりそうな気もします。
まりおさま
「♪ヒロシです…。算数ラボが大型書店になかとです。ヒロシです…ヒロシです…。」
別の書店に行ってみます。多分10級だと思います。
時計の単元が始まるまで、全集中で小1の算数をやっています。実は時計も不安なんですが…。
またよい教材があれば教えてください。よろしくお願いします。ありがとうございました。
こんにちは。
肯定ペンギンさん
「♪ヒロシです…」からの始まりに、大爆笑しましたよー(≧∀≦)
ヒロシさん、、、「算数ラボ」は、私も本屋さんでは見かけた事が
なかとです。いつもネットで入手しとるとです。
でも、手に取り中身の確認が出来ないのは不安。。。
そんなヒロシさんには
「そんなの関係ねー」の小島よしおでイッテみるのもアリかもです。
…なんて、算数ラボの回し者ではないですよー(^◇^;)
「田中先生の算数絵解き文章題」が新品ではもうない!!とは…
紹介しておきながら、すみませんでしたー。。。反省です。
時計の件ですが、我が家は市販のドリルではなく、肯定ペンギンさんも
ご存知の既出ですが「ぷりんときっず」「ちびむすドリル」を使ってました。
ネットの無料プリントは、子供の弱い部分を見つけた時、ドリルを買いに
走らずとも、その場で直ぐに用意出来る所がすごく良いですよね♪
1〜2年生の時にはよく使ってました。
肯定ペンギン様
こんにちは。
同じ小二の子を持つ親として、なにかお力になれないかと思いながら拝見しておりました。
お子様の計算間違いの件、見当違いなら申し訳ないのですが、もしかして計算を丸暗記しようとしていませんか?または数が大きいときにそういった様子が伺える、とか。
数量感覚が十分に育っていない場合、簡単な計算から丸暗記に頼ることになると、我が家で取り組んでいる教材の解説DVD内の説明にあったと記憶しており、もしかして肯定ペンギン様のお子様が当てはまるのではないかと気になったのです。
また、息子の学校では昨年一学期には「いくつといくつ」という単元で、毎日一回の暗唱を宿題に出していました。当時、計算を丸暗記するのと同じことをしているのでは?と疑問に思いつつ息子の暗唱に付き合っていました。授業中児童を並ばせて暗唱の時間をとるより、手を動かして数の合成分解の操作を繰り返した方が身につくだろうにと、今でも思っています。
もしも一年時に同様の暗唱があったなら、丸暗記を疑ってもいいのではないかと考えますが、いかがでしょうか?
ぶたのこ様
コメントありがとうございます。
うちは暗記ではなく毎回計算をしているようです。
繰り上がりが出てくる前までは順調で、繰り上がりはさくらんぼを予習していましたので、繰り上がり・繰り下がりとも拍子抜けするくらい順調でした。(去年は休校の影響か、繰り下がりに入るのが早く、予習をする前に繰り下がりが始まってしまいました。)ただ、この時期はまだ手で計算することが多かったように思います。
うちの学校も計算カードがあって、毎日家で暗唱、学校でもたまにテストがあったようです。文章題が始まったあたりから計算ミスが出始めました。
計算カードをやっているのにミスをするので、三学期からは暗唱をする代わりに計算プリントを1枚させましたしました。時間は計らず、100点を目標にやらせましたが、足す数が大きい計算や、3つの数字を足す計算で間違えます。
繰り上がりはさくらんぼで解いている時と、7+8→2+(5+5)+3→2+10+3→10+5→15でやっていることがあって、手計算していた時の名残だと思います。これだと間違えますよね…。いつか数量がわかれば普通の手順でできるようになるかと思い、あえて口出しはしていません。
私も主人もそろばんをやっていて考えずに計算できてしまうので、教えることができません。2年生も計算カードがあり、考えながら暗唱する子は合格できないと聞きます。今も毎日1年生の計算をやっていますが、ここまで来たら暗記でもいいのでは?とも思います。今はこんな感じです。筆算が始まるので焦っています。
肯定ペンギンさま
横からすみません。
計算について思ったこと1点。途中から参加なのでご家庭の事情については考えておりませんので先に失礼があれば謝っておきます。
コメントから考えるに、お嬢さん、気が散ってしまうタイプなのかなと思いました。先生のお話も途中で他のことに気を取られ、部分部分だけ覚えている。
少し背伸びしたいお嬢さんかな?
おはじきや百玉そろばんが格好悪いなら、お母さんのジュエリーや化粧道具でもいいんです。子どもが興味を引くもので、まず数の概念を教える。口紅は何本?指輪は何個?という具合に。目で見てわかる数、それが具象として頭に入れば、数として抽象化され、3+2であれば、基礎化粧品3とイヤリング2という理解に繋がる。
おやつでもいいんですよ。チョコレート7個とクッキー8個のうち、10引いた数だけ好きなものを食べていいよ、とか。瞬時に計算できなければ、好きなものを順番に1個ずつ取っていくと10と何個かのかたまりが出来る。そういった日常のお母さんとのふれあいのなかに算数の基礎があります。
おそらくペーパーで学ぶより、身につくのが早いと思いますヨ。
家のお手伝いも、算数と理科の宝庫ですから、いろいろと手伝ってもらいましょう。
参考になれば幸いです。
肯定ペンギン様
返信ありがとうございます。
お子様は、暗記せずに毎回しっかり計算されているのですね。
でも、文章題や、大きい数や3つの数の計算で間違えるのですよね。
正直、数量感覚を先に育てた方がいいと感じますが、どうでしょうか。
さくらんぼは、数の合成分解で覚えた数字が書ければ答えがでますが、文章題や3つの数の計算は数量感覚に乏しければ解くことは難しいでしょう。
もし取り組まれるとしても、自分で手を動かすようお子様に言っても抵抗が強いかもしれません。その場合は親御さんが手を動かして、視覚で量や量の変化を感じさせるといいかもしれません。
同じ色形大きさのおはじきと、ひとマスにおはじきが入るくらいの10×10のマス目を書いた台紙があれば、1年生の範囲なら足りると思います。
以上、見当違いのアドバイスでしたら脳内deleteお願いします。
皆さん コメントありがとうございます。
肯定ペンギンさん。
すららを見てみました。お値段は良心的かなって思いました。
計算の話ですが、この時期で躓く子は一定数います。
だから、肯定ペンギンさんが焦る気持ちはとっても分かります。
数のイメージは、ぶたのこさんやぷりんさんが書かれている通りで、まずは数のイメージがしっかりしていないと、伸び悩むかと思います。
やり方は、お二人が書かれているので割愛しますね。
次のステップになるであろう暗唱ですが、うちも計算カードはタイムを測定するので、わざわざ分解して考えて答えをだすようなことはできないです。
これこそ、瞬時です。
もう数字をみただけで答えが浮かぶ。
ここまでのトレーニングが必要です。
計算の回数をこなしていく過程で覚えちゃうはずです。
うちの子達は11×11や12×12なども瞬時に出るようです。
簡単な問題は瞬殺というわけです。
無責任かもしれませんが、出来ている(た)のですから、大丈夫な気もしてきました。
まりおさんの息子くんの例もあるように、少し混乱しているだけなのかも!
この計算は算数→数学へと入っていっても、本当に大事になってきますので、焦らずしっかり取り組んでほしいと思いました。
ちょっとでも出来たら褒めて(ここがポイントですね)、頑張ってほしいです。
うちは小学6年生で中学のことは聞いた話しかわからないのですが、コメントさせていただきます。
地方都市の市内で一番内申が取りにくい中学に進学する予定です。
卒業生の親から聞いた話だと内申が多少足りなくても、公立志望校は受けられる。もちろん学力テストの結果が志望校を上回っていることが前提。
他地域ではわかりませんが、この辺の高校は偏差値ががっつり取れて、普通に中学生をやっていたら、志望校は大丈夫みたいです。つまり、内申のために定期テストをすんごく頑張る(金払う)よりも、高偏差値を取れる実力をつけることの方が楽で安あがりだと思います。みんな内申点に振り回されているのが現状ですが。
偏差値を上げる方法は塾が向いてる子、独学が向いてる子、親がしっかりしている子、私はどれでもいいと思います。管理人さんが子供たちに身に着けてほしいと思っている「瞬発力」「認知力」「無知の知」「トライアンドエラー力」みたいなものはもう充分備わっているような・・・・。志望校に合格することを期待しています!
Wさん 初めまして。
色々キーワードを書かれてますが、きっとこのサイトの常連さんですね。
コメントありがとうございます。
内申のネックは、やはり実技も取らないといけないところでしょうか。
高偏差値が取れる実力をつけるためには、定期テストは満点を目指すといいと思います。
うちは、社会で1年の1学期、2年の1~2学期と手を抜いたのが、そのまま理解不十分となり、高校入試の過去問も聞き返したぐらいの点数でした。
2年の3学期からテコ入れ中です。
一番内申が取りにくい中学でしたら、レベルも高そうなので、差が出るように100点阻止問題(入試レベルの難しい問題)が紛れ込んでいるかと思いますので、頑張ってください。
私も内申より実力と考えてます。
実力とともに、内申もついてくる。
話を聞く限り、逆な子もいるようですが、実力が先であってほしいですね。
内申美人は大学入試で詰んでしまうので。
ちなみに、まだ下の2人はこれからですが、愚息に関しては、ご存じの通りかなりイレギュラーです。
これからすこしずつ軌道修正をしていきます(汗)。
管理人様、ぷりんさま、ぶたのこさま
コメントありがとうございます。こんなにも気にかけていただいて、娘は幸せな子です。
あのコメントを書いたときは、知人のお子さんで、学習障害で小3まで足し算ができずに6年間イジメられ、算数なしで中受をして合格された方と話した直後で少しナーバスになっていました。ご心配をおかけしています。まりおさま、詩人の母様に励まされ、管理人様にもアドバイスをいただき、今はだいぶ前向きになれました。
数については、お金(ドリルも)、食べ物、幼児のパズル道場「かずと思考力」(ドリル)など、やれることはやったと思います。どうしても数量が脳に沁みこまない印象です。強力撥水加工レベルです。お金の実物(小銭)だと100までの足し算、100円単位の1000円までの足し算ができるのですが、数字だけになるとダメみたいです。5円玉、50円玉、500円玉を混ぜても計算できます。小銭が好きなので、お金の枚数(金額ではなく)でやってみます。
小さいころから、お菓子の大小はわかるので、物量はわかるのですが…。ピザが好きなので、8分の4は2分の1だね、みたいなことも言います。アイロンビーズも幼稚園の時から図案を数えて一人で作ってます。
ぷりんさまご指摘の「集中できない」はご明察です。計算プリントの計算の数が30を越えると、必ず2問目か3問目を間違えます。後は正解か、裏面の一問を間違えるかです。
面倒なことが大嫌いで、最初は気が乗らないのが丸わかりです。文章題に至っては、数字を拾うだけで思い込みで文を読んで解いています。色々なことに気になるようで、車に乗っていても車窓からいろんなものを見つけます(-_-;)
管理人様
すららは識字障害であれば使ったのですが、現実ではこういった補助は受けられないので、できる限りテキストで理解できるように頑張ってみます。タブレット学習は知ってしまうと後戻りができないという危機感を持っています。
計算カードはやっぱり暗記ですよね。そこは割り切ってやります。
まりおさま
書店であの音楽♪とともに「ヒロシ」が下りて来たとです。そちらでも見かけないと聞いて安心しました。お薦めの本はネットでだいたい3000円くらいみたいです。
参考のため時計の問題集を見ましたが、ドリル一冊時計だと使い切れません(^^;)今どきの無料プリントは優秀ですね。
肯定ペンギン様
小二は学童期ではありますが、脳の発達としてはまだ幼児期で、具体の世界にいるのだそうです。
幼児期、数を獲得する時期には、おはじきなど実際に動かせる具体物が必須です。
数の合成分解や簡単な足し算引き算も、具体物を利用して繰り返していきます。
数字は数量を表す記号であり、抽象的なので、幼児の学びには不向きなのです。
教科書での学びが始まる時期(年齢)は、具体物と数字が一致するような、それこそ数字を見て数量を頭の中に思い浮かべたり、逆に具体物を数字に置き換えたり、といった経験を積みます。
繰り上がりの足し算や繰り下がりの引き算も、数字ではなく具体物で計算することを繰り返します。
幼児期に具体物で数を操作した経験に乏しいと、数字と数量の関係が曖昧になり、文章題を読んでも頭の中でイメージできず、式が立てられなかったり、計算間違いをすることになります。
数字と数量が一致すれば、計算間違いもなくなり、計算に時間がかからなくなり、計算カードの暗唱は丸暗記することなくクリアできるようになるはずです。
ぶたのこさま
コメントありがとうございます。
小銭、100玉そろばん、カラーそろばん、こぐま会の今は売っていない「かずのおけいこ」あたりをやっていこうと思っています。小銭以外はすべて全力で抵抗されたのでうまくいくかわかりませんが、週末ぐらいから着手する予定です。10の合成・分解の手遊びは嫌がらずにやりましたが、身に付きませんでした。
暗記せずに計算は、そろばんをやっていたのでわかります。コロナでなければそろばんをさせていたかも知れません。
肯定ペンギン様
こぐま会の「かずのおけいこ」、我が家にもありますよ。とてもいいのに絶版になっしまって残念に思うドリルです。我が家も付属のおはじきと一緒に大事にずーっと本棚に置いてます。
取り組みの際、気をつけていただきたいことを書き忘れていたのですが、数が増えて繰り上がっても、小銭の両替やそろばんのように、十の位を作らないようご注意ください。つまり、10×10のマス目台紙の縦一列におはじきが10個並んだら、すぐ右横におはじきを並べていくのです。
今回は計算ではなく数量感覚を育てることが目的なので、位を作ってしまうとだめなんです。
また、10×10のマス目の台紙ですが、例えばおはじきを8個並べたら2マス空くので、「あといくつで10になる?」と聞いても視認で答えられて便利ですし、階段(左から1、2、3…10までおはじきを並べる)が作れるので、眺めるだけでも10の合成分解を感覚で覚えられるようになると思います。
以上、肯定ペンギン様親子の健闘をお祈りします。
ぶたのこさま
コメントありがとうございます。やり方を間違えるところでした。
位を作らないということだと、一番いいのは1~20までの横一線のスケールにおはじきを置くやり方ですね。うちも一時やっていました。まずはこれからやってみます。10のところに印をつけて、繰り上がりがわかるようにします。
以前は百玉で、一段目に足される数、二段目に足す数を置いて、下から上に玉を動かすというのもしていました。百玉の使い方もいろいろあるようですが、百玉自体がかっこ悪いと思っているので、階段を作るとかはできませんでした。
「かずのおけいこ」は付録はいらないので冊子だけでも再販してほしいくらいの名著です。使い終えたら誰かにあげようと思っているのに、なかなかそうはいかないみたいです。この冊子でも繰り上がりになったとたんに拒否されました。
肯定ペンギン様
ついに私のMacの予測変換に「肯定ペンギン様」があられた!
こんにちは。何度もすみません。
10×10のマス目台紙へのおはじき等の置き方は、以下の通りです。
●はおはじき、□は空欄、です。
例)8
□
□
●
●
●
●
●
●
●
●
例)14
●□
●□
●□
●□
●□
●□
●●
●●
●●
●●
例)26
●●□
●●□
●●□
●●□
●●●
●●●
●●●
●●●
●●●
●●●
例)1〜10の階段
□□□□□□□□□●
□□□□□□□□●●
□□□□□□□●●●
□□□□□□●●●●
□□□□□●●●●●
□□□□●●●●●●
□□□●●●●●●●
□□●●●●●●●●
□●●●●●●●●●
●●●●●●●●●●
私に説明能力がなくて、テキストではなかなかイメージが伝わりにくいようで申し訳ありません。
ぶたのこさん 肯定ペンギンさん コメントありがとうございます。
ぶたのこさん、ステキ過ぎます。
数のイメージが出来ないと、ここで算数は詰んでしまうので、本当に大切なところだと思ってます。
肯定ペンギンさんだけじゃなく、他の方でも参考になっている方も多いかなと。
ちなみに、学年が上がる毎にどんどん桁が増えていくのですが、それがまたついていけない子が増えるようです。
4年で億以上の単位、3年は億までの数だったかな。
担任の先生は、1000を超える数ですら、イメージがつかない子がいるので、買い物に連れて行ってレシートを見せてあげてくださいとまで言ってました。
ぶたのこさま
うちのPCもぶたのこさまを覚えています(^^)
おはじきは縦置きなんですね!10の横とはそういう意味でしたか。百玉そろばんをイメージしていましたが、そういえば、「かずのおけいこ」「パズル道場」は縦でした。打っても響かない私に伝わるように、時間をかけて考えてくださったことがわかります。本当にありがとうございます。
今日は雨なので、頑張ってやってみます。夫に頼んだら2回でメンタル崩壊したので、私がやるしかありません。一年前に大荒れした数量感覚は、私としても気が重いです。
こちらのスレにこの話題を置いておくのがもったいないなと思います。小1スレだとよかったです…。
管理人様
これだけ投稿しておいて今更なんですが、肯定ペンギン様親子に負担をかけてないか、親子関係に亀裂が入ってないか気になって挙動不審になっている小心者です。
超有名なモンテッソーリ教育の代表的な言葉に「敏感期」がありますが、多くの人が思い浮かべるのはイヤイヤ期の敏感期でしょうか。
でも幼児期には数の敏感期もあって、この「数えたい!」「もっと大きい数を知りたい!」という時期に、繰り返し何度も数え、さらに大きい数を目にした子というのは、やはり数量感覚に優れ、触れたことのないもっと大きい数も認識できるのだそうです。
息子はモンテッソーリ教育を受けたわけではありませんし、私が息子と某ピからはじまる教材に取り組んでいる間に感じたことですが、ぷりん様が書かれた通り、数や数量は身近にたくさんあります。ただ、今の子供たちは、親世代が子供の頃よりも一度に触れる数が少なかったり、動画やゲームなどの楽しみが先にきて、袋いっぱいのどんぐりや一つの苗から取れた朝顔の種を数えるといった、数を自分のものにする時間がたりなかったりするのかな、と思うのです。
10×10のマス目台紙、便利ですよ。
おはじき使って1〜10の階段を作ってもいいし、繰り上がりや繰り下がりの計算にも使えるし、2年生ならかけ算にも使える。九九範囲ならあまりのあるわり算だって計算できちゃう。
数量感覚に乏しい子だったら、今日はお父さんの年の数だけ並べて、明日はお母さん、おばあちゃんやおじいちゃんの年の数を並べてもいい。もちろん、100歳だって並べられる。親御さんが置いてもいいし、お子様が置いてもいい。
嫌がるようなら、視界に入るところにこっそりと。
教えず、無理強いせず、決して怒らず。これがなかなか難しいですが。
ぶたのこさん コメントありがとうございます。
初っ端の文面に思わず笑ってしまいました。
大丈夫です。
だって、ここで舵取りを間違えると、この先はとんでもない状況が待ってますので。
肯定ペンギンさんは、分かってらっしゃるからこそ、きちんと耳を傾けられているのだと思います。
>数を自分のものにする時間がたりない
これは本当にそう思います。
そういえば、ぶたのこさんのコメントで思い出しましたが、うちの子達はひまわりの種を一生懸命数えてました。
気が遠くなるような量でしたが、夢中になってましたわ。
それが、ちょうど小2だったと思います。
なるほどですね。
ぶたのこさま
ご心配をおかけしています。週末にいろいろやってみました。新学期が始まっても、まだ小1の範囲が正答できないことで少しは危機感があったのか、週末には子供がおはじきを自分から持ってきたこともありました。ばらばらのおはじきを数えるのが遅い、ドリルの7+6=13は即答するのに7+□=13は ぱっと答えられないなど、やはり数量感覚に欠けるようです。
それに加えて本人の自覚が足りず、ここ半年ぐらい、「計算でつまずくと2年生で理解できなくなるから間違えないことが大事だ」とか「どうすればミスが無くなるのか」などを話し合ってきましたが、本人は「30問中、1~2問しか間違えなかった。」「テスト時間中に全部解いている。」といった認識らしく、正確さや迅速性の価値などは理解できないようです。正解を口で言っていたのに書き間違う(計算しているのにしゃべっている時点で集中してません)、思い込みで問題を読むなど、ぷりんさんがご指摘されたような集中力に欠けることも頻発しています。
4月に入ってからは、国語をストップして小1算数ばかりでしたが、もうすでに時計の範囲が始まるため、、小2の範囲に取り組みつつ、細々と小1計算やおはじきを続けて行こうと思います。ぶたのこさま、ぷりんさま、管理人様、どうもありがとうございました。いつか、計算ができるようになったと報告できればいいのですが…。
追記です。
ぶたのこさま、大丈夫です。亀裂は入っていません。年長後半から先週末まででやるべきことはやりきりました。それでこの結果であれば、今の子どもの能力でやっていくしかないと腹をくくりました。後は本人が自覚するか、現状の取り組みを続けて事態が好転することを祈るばかりです。長期戦です。
肯定ペンギン様
返信ありがとうございます。
お子様自らおはじきを持ってこられたとのこと、とても大きな前進ですね。自分は無敵だ万能だと信じている時期の子供にとって、不足を認めるのは辛いことだったと思います。親としては、危機感を持つ前にやってほしいと思ってしまいますが。
今後ですが、実物のおはじきで数の操作を続けていると、頭の中でおはじきを動かせるようになる時期が来ると思います。そして頭の中のおはじきを使って計算を繰り返していると、自然と頭の中のおはじきが消えて、数字だけで計算ができるようになるのだそうです。
時間はかかるかもしれませんが、この段階まで来た時には、計算の正確性やスピードはクラスでも上位に入っていると思います。元々自分でしっかり手順を踏んで計算してこられたお子様ですから、きっと大丈夫です。
…苦悶式?
…しらん!!
あと、時間のひき算です。
8時20分の30分前、といった問題は、一旦20分前に戻って8時0分にし、残りの10分を引く考え方のほうが理解しやすいそうです。教科書ではなぜか、7時80分ー30分で計算するようですが。
以上です。肯定ペンギン様親子に幸あれ〜
ぶたのこさま
温かいお言葉をありがとうございます。
子どもが数量を嫌がるのは、面倒だからではなく理解できないからだと思います。教えているこちらは、泳げない子の頭を押さえつけて水泳をやらせている感覚で、やり切れません。
これからやる算数の勉強に計算が必要なことを説明しても子どもには理解できないようです。でも今回おはじきを持ってきたことをそのようにおっしゃっていただいて、子供に対する私の理解も欠けていたなと反省しました。
今年は宿題させるのが精いっぱいで、今、既におはじきの時間が取れません(涙)。週末や時間がある時に、少しずつやっていきます。漢字のお直しが多く、国語の「対応する言葉を線でつなぐ問題」で定規を使わないとやり直しをさせる先生に当たり、以前に増して宿題をするまでに時間がかかります。
苦悶の体験を考えていましたが、今行っても間違いなく「+1」が連続するレベルで査定されると思うのでやめます。少しはショックを受けて欲しかったのですが。
時間の引き算は日常生活で話題になりにくく、教えるのも難しいです。7時80分は初めて聞きました。時計は一問で時間と分の計算ふたつをするので、本計算ができないのは本当に致命傷です。今後は長さ重さや面積、速さなど目白押しでめまいがします。
ピで始まる教材をされていたのですね。親のレベルが高くないと使えない教材だと思い、うちには無理でした。憧れます~。
肯定ペンギン様
おはじきを使う時間がとれなくても、数を数える機会はたくさんあるので大丈夫。
例えば、焼いたポークビッツを数えながら取ってみたり、おかずにする予定のミニトマトの数を指定して持ってきてもらったりするのはどうですか?自分の中に持っている数量であれば、負担は少ないと思います。他にも、家の窓の数を調べてみたり、階段の段数を数えてみたり。親と一緒に数えて大きい数を体験させるのもありだと思います。
教えようとしなくていいんです。まずは親がやってみせること。そして親子で一緒にやってみることが大切です。
時計ですが、家にアナログ時計はありますか?時刻の読み方だけでなく、針の動きも理解していますか?
時計のひき算は、うちの息子も最初は間違えていましたが、ゲームが好きなので「時よ戻れ〜」と呪文風にしてみたらイメージできたのか、模型を使って繰り返しているうちに間違わなくなりましたよ。
ぶたのこさま
肯定ペンギンさまとのやりとり、興味深く拝見しています。
私も小2の母です。
子供とのやりとりでふと思ったことですが、パッと見て5個ぐらいか、10個ぐらいか、20個ぐらいか、アバウトな数量を推測するのも案外大事かな?と思ったのですがいかがでしょうか。
ちなみに我が家で数量感覚を身につけるのに役だってるのはいちごですかね〜?
4人家族なので1人いくつもらえるのかいつも必死に数えてます。笑
最近20ぐらいのまとまりが予測できるようになったのか、全部数えなくてもぱっと見て「1人5個ぐらいかな〜」と答えるようになりました。
おかげでついついスーパーでいちごに手がのびてしまい、エンゲル係数高めです。
肯定ペンギンさん
ぶたのこさん、詩人の母さん コメントありがとうございます。
>面倒だからではなく理解できないからだと思います。教えているこちらは、泳げない子の頭を押さえつけて水泳をやらせている感覚で、やり切れません。
肯定ペンギンさん、辛いですよね。
うちも下の2人は覚悟して取り掛かったので、この例えはとても理解できます。
過去のコメントで気になったところがあるのですが、
>お金の実物(小銭)だと100までの足し算、100円単位の1000円までの足し算ができるのですが、数字だけになるとダメみたいです。
例えば、絵が20個30個と並んでいたら、足し算引き算が出来るのかなあ。
数量の感覚はもう既にあるような気もしているのですが。
時計は前から居座っている方ならご存じの話ですが、うちにはアナログ時計がありません(汗)。
はい、3人とも怪しかったですよ~。
あった方がいいですね。
定規の話はうちの子達もやり直しを食らってました。
漢字もこの頃から増えるので、時には泣きながらやってました。
3人ともです。
これから苦労するかもしれませんが、娘ちゃんだけじゃないことをお伝えしておきます。
詩人の母さん。
いちごは争奪戦ですね。
詩人の母様
いちごの季節ですから、一パックあたりのいちごの数を推測するのは楽しくていいと思いますよ。同じ大きさのパックでも、大きい粒のいちごならいくつ、小さい粒のときはいくつと、経験から予測しているだけでなく、その後数をわけるという割り算(時々あまりあり)の基礎にもなりますから。お子様が関心を持つことを、楽しく学ぶことが大事です。
管理人様
お金は位があがると両替で見た目が変わるだけでなく、数が少なくなるため数えやすいのだと思います。だから、数量感覚でいえば、100円玉を見て1円玉100個が思い浮かぶかどうか、ということになるのではないでしょうか。
そして肯定ペンギン様のお子様は、もうひと押しで脱皮できると信じてます。計算は手順を踏んでできているのですからね。ていうか、二年生の計算範囲を暗算でやれば一年生範囲はできるようになるっていう幻想もあったりなかったり…。
ぶたのこさま
昨日はフレンチトーストを16切れあると言ったので、どうやって数えたか聞くと、「8+4+2+2」と独特な答えが返ってきました。^^;)「5切れ食べて迷路を作った。」「7切れ食べるとゴール。」など、ちょっと数えブームが来たようです。
「学校の先生がもう50回も怒っている」というので、私が「17+17+17=51だから週に17回怒っているね。(本当はまだ2週間ですから25回でした…。)」と言うと、「7+8+6(+30)かも知れないよ。」と言い返してきたので、こういった言葉遊びができたらいいなと思います。もう一押しと言っていただいて、しぼんでいたやる気が戻りました。
時計はアナログがあるのでいいと思っていたら、子供のに「数字がないからわからない」と言われ、慌てて小さいものを買いました。廊下の給湯器の操作パネルがデジタルで、そちらばかり見ていてあまり効果はありませんでした。
詩人の母様
概数は大事ですよね。これも小さいときにやりたかったです。「この数字はおかしいよね?」と思える感覚がないと、間違いに気づけないと思います。生活の中でちょくちょく入れていきます。
それと、う〇〇ドリルを教えていただいて書店に行ったらなんと!低学年の文章題が出ていて、小1を買いました。まだ前半なのですが、後半の問題を間違えないかひやひやです。イラストが多く、2ページ連続イラストの時もありますが、嫌がらずにやっているのでよしとします。本体価格1150円もします(怒)
管理人様
お金に並々あらぬ興味があり、興味があると苦にならないんだなあ、と変なところで感心しています。5円、50円がワンクッションになって数えやすくなるんですかね…。
15-7も「10-7は3ッ♪3+5は8ッ♪」と、とにかく手順を踏んでいます。
他にも、7+8=15 がわかって、7+□=15がぱっと出ないのは、やはり数量感覚が足りてないのだと思います。もう間に合わないので、筆算多めで小1足し算を兼ねる作戦しかありません(汗)
筆算も定規で線を引くのでしょうね。考えながら書くのが苦手のようなので、頭が痛いです。
肯定ペンギン様
ここ数日、調子を取り戻されたようですね。
コメント投稿の数でわかります。よかったよかった^^
また、お子様との数のやりとりについても、楽しそうなご様子に安心しました。
数を楽しむ姿勢が素直でかわいらしいと思いますよ。
7+□=15がパッと出ない、というのは、ある程度仕方ないと許容しましょう。
即答できるレベルの子は、7を見た段階ですでに3が思い浮かんでいる状態だと思います。「あといくつで10になる」かを常に意識する必要があるので、もうしばらくおはじきの操作(10×10のマス目台紙があるとなおよしです)を続けてみてください。おはじきを7個置いたら、上に3マスの空欄ができる、というように視覚で印象付けていく感じですかね。
先日、入学以来初めての授業参観があり、一年生の足し算の復習を見ましたが、繰り上がりは数えたしでやっていてびっくりしました。さくらんぼどこいったのー!
ぶたのこさま
なんでもお見通しで驚きです。
相変わらずの低飛行ですが、子供が先生のご指導に慣れてきたようで、夕食前に宿題が終わるようになりました。熱心な先生で、連絡帳にまで朱書きが入ります。メリハリが利いているいるので大人が見れば納得なのですが、去年の先生が1年生はのびのびとできるようご指導される方だったので、子供にとっては急なダメ出しがショックだったみたいです。
「あといくつで10になる」のご説明に納得です。10の合成、分解はプリントでは問題なくできるのですが、繰り下がりとなると短期記憶が弱いのか、10から引いた残りを記憶できていないのでしょうね。プリントにメモしてくれればいいのですが、メモするぐらいなら×になるほうがマシな感じです。何のプライドなんでしょうか…。モノで10の合成をしたらマシになるかも!と思いました。
調べたら数え足しだと位取りができないそうですね。私がやっていたのはこれに近かったかも知れません。
肯定ペンギン様
「あといくつで10になる」
ここ大事ですよー。
テストででますよー。
短期記憶が弱いなら、お子様が楽に解答できるレベルの計算問題を口頭で出してみるのもいいかもしれません。二つの数をちゃんと覚えて正答できればok、最初の数を覚えていないようなら少なめの数で練習をしてみてください。
また、お子様に文章題を見せずに、肯定ペンギン様が問題文を読み上げてお子様に解かせることも、短期記憶の向上に繋がると思います。文字を読めない時期はこうやって解いてましたよね。
実は、ちょっとの間頭の片隅に置いておくことも、練習が必要なんですよね。そういえば、しりとりも短期記憶ですよね。計算に飽きたらしりとりです。
あと、□のある式の解き方ですが、足し算は足して、ひき算は引いて考えます。
7+□ =15なら、「7にあといくつたせば15になる?」という問いかけ、15−□=7なら、「15からいくつ引けば7になる?」という感じです。□−8=7であれば、「いくつから8引いたら7になる?」でしょうか。
大人はもう習った後なので、□=15−7にしたり、□=7+8にしてしまいますが、こう計算すれば答えが出るよ、とわざわざ教えないこと。数量感覚があれば、式を書き換えて計算しなくても答えは出せますから。もちろん、子供が自分で気づいてしまった場合は否定せずそのまま計算させて構いません。
肯定ペンギン様以外の方が読まれた場合に参考になればと思い書いてみました。
ぶたのこさま
10の合成は夏休みにプリントでやって、これだけはできるようになりました。改めてモノで視覚化しようと思います。
夜寝る前によくしりとりや計算をやります。計算は10+10までですが、人とやる時は数を覚えているのかも知れません。テストや宿題で自分だけでやると、意識が飛んでしまうのかも~( 一一)
文章題読み上げは簡単なのをやってみます。□のある計算は、すでに解き方を習ったみたいですが、ぶたのこさまの問いかけの方が理解しやすいと思うので試してみます。
そういえば、夫がう○○ドリルを一年生用だから終わっているものと思って片付けてしまい、見当たらなかったのでグレードアップ小1文章題をやらせたら嫌がらずに解いていました。ぶたのこさまや管理人様によくなっていると言っていただいても実感はなかったのですが、少しずつ前進できているのかも知れません。ありがとうございます。
肯定ペンギン様
先日投稿したあとに思い出したのですが、1年時の個人懇談で担任の先生から伺ったことですが、国語も算数も問題文を声に出して読むことを勧めておられました。国語の音読と同様に、算数の文章題も声に出すことで耳から情報がはいり、イメージしやすくなるのだそうです。学校のテスト中に音読は無理ですが、家庭学習ならできることですし、一度間違えた問題であってもお子様自身が声に出して読んでみたら、案外すんなり解けるかもしれませんね。
また、しりとりですが、Z会4月号で「おぼえてしりとり」というしりとりがありました。
例えば「しりとり」→「りんご」→「ごりら」→「らっきょう」→「うさぎ」なら、通常のしりとりなら一人が一つの言葉を言っていきますが、この「おぼえてしりとり」は、2番目の人は「しりとり」と言ってから「りんご」と答え、5番目の人は「しりとり」から「らっきょう」まで言ってから「うさぎ」と答えるのです。
大人がわざと子供の知らない言葉を言ってみるのも、短期記憶の練習として楽しい遊びかなと思います。
このところ、肯定ペンギン様親子の取り組みの成果がでてきましたね。お子様頑張ってる!すごい!えらい!
グレードアップ問題集が解けるほどなら、もう私のお節介は必要なさそうですね。うれしいうれしい。
それでは、これにてどろん^^
ぶたのこさま
そのしりとり、多分私が負けます^^;
さすがZ会ですね。今晩やってみます。きのうは「ごちそうしりとり」でしたが、2巡目でつまずいて、「森で見つけたキイチゴのケーキ」と言っていました。
文章題の音読は以前試してみましたが、余り効果がありませんでした。私もそうなんですが、音読すると読むことに意識が取られ、意味が頭に入らないようです。
書店で見つけた「つまずきをなくす 小1 算数 文章題」という本で、問題文の文節ごとに「/」を入れる方法があり、今日から試そうと思います。スラッシュがあると、私でも黙読のスピードが落ちます。
グレードアップはひっかけ問題風ですね。今8回目で、1回に見開き2ページ分をやりますが、番簡単な一問目のみ間違えてます。2ページ目は解けているので、本人の意識の問題のようです。以前グレードアップをやっていたときは発狂して、代わりにハイレベ小1を(できる問題だけですが)やったので、文章題への耐性がついたのかも知れません。ハイレベの方が難しいと思っていたので「うちはグレードアップだけでいいわ。」とやらせたのですが、グレードアップの文章の書き方が独特なのがダメだったのかも知れません。
今日一年生のドリルの整理をしていて、たまたまブロックがいくつあるかという問題をみつけてやらせてみると、即答はできないようでしたので、パズル道場の天才脳ドリル数量感覚初級をやりたいところです。算数がそろそろ単位に入るので、ここのつまずき具合(←つまずく前提)を見て決めます。おはじき、ブロックは本当に嫌がるので、買って終わりかも知れません。
またつまずいたら、こちらで呟きますのでアドバイスよろしくお願いします。
お世話になっています。
うちの近所の塾がどこもかしこも、高校進学実績はいいのに、大学進学実績がイマイチなのは、こういうことか、と納得しました・・・。
また、いい高校入っているのに、高校以降振るわない生徒が多い理由もこういった面倒見がいい塾のせいなんでしょうね。
ゴールが高校合格・・・。
うちの公立小も、中受しないにも関わらず、5年生あたりでは全員塾に行くような環境です。
なんとか塾なしでいきたいものです・・・。
悩める母さん コメントありがとうございます。
書きたかったことがありましたので、丁度良かったです。
都会のトムソーヤにハマる小2の子なんて、なかなかいないですって。
今、末っ子(小5)が読んでいるぐらいです。
上の2人も小5だったような気がします。
はやみねかおるさんの本、面白いですよね。
お子さんなら塾は要らないと思いました。
受験しないなら、なおさら。
合う塾がないんですよ。
自分で勉強を進めていける子だと思いますので、このまま気に入ってるZ会で頑張ってほしいですね。
いいですよ~。塾なし。
周りに比べて、本当にお金がかかってませんので!
自分で理解していく力、あれこれ試行錯誤しながら確立した勉強法って最強なんじゃないかなって思っています。
管理人さん
コメントありがとうございます!
管理人さんにそう言っていただけるとなんとかなるような気がしてきます。(ハイレベにまだ取り組めてませんが・・・。)
私は今日初めて都会のトムソーヤ読みました。
確かに子どもがハマるのも頷けます。うちの子は今2巻の途中です。
受験をする予定はありません。お金もないですし、田舎なので、そんないい私立もありません。
うちの子はなぜかZ会がすごく好きなので(管理人さんのお子さんもそうですよね?)、ずっとZ会でやっていきたいと言っています。
「自分は頭良くないけど、Z会のおかげで勉強できてる」と言っています。頭良くないことはないと思うんだけど・・・と思うのですが(良いとも言えない気がするけれど)、「十分すごいよ」と言っても、「いや、Z会がすごいの!」と反論されます。
信者かもしれません・・・(汗)。
こんにちは。
小学校低学年ですでに家で勉強をみられなくてどうする!という教祖様の教え(?)の下、幼児から低学年向け数量感覚による繰り上がり足し算、かけ算、わり算を投下します。
まずは以前投下していなかった気がする幼児コースの足し算から。
準備するものは、2×5のマス目を2つと、おはじきを20個ほど。
1)繰り上がりの足し算の前に、1枚のマス目をつかって数量を見せる。
おはじきを置いたら子供に数を言わせる。□空き ●おはじき
□□□□□
●●●●□ 例)おはじき4個
●●□□□
●●●●● 例)おはじき7個 のように置く
2)何回か繰り返して、6〜10は、5と1〜5に分けられることを認識させる。
3)10までの足し算を繰り返す。
1枚目のマス目に足される数、2枚目のマス目に足す数を置く。
足す数を足される数の続きに置いて、下の段が埋まったら(5つ並んだら)上の段に置く。
□□□□□
●●●●□ + ●●●□□
=
●●□□□
●●●●● 例)4+3=7
4)繰り上がりのある足し算(5以上+5未満の場合)
10までの足し算の時と同じように置く。
● ←マスからはみ出ても整列させてください
●●●●●
●●●●● 例)4+7=11の場合
5)繰り上がりのある足し算(足す数足される数両方5以上)
1枚目のマス目と2枚目のマス目におはじきを置いたら、隣同士に並べる。「5足す5は10!!」
●●●●□
●●●●●<5足す! + ●●●●●<5は!
=
●●●●□□□□□□
●●●●●●●●●●<10!! 例)9+5=14の場合
学校で習うさくらんぼを使うと、5を1+4にわけて、9+1をしてから4を足す流れでしょうか。6+7や6+8なんかは、5と小さい数にわけて、5同士小さい数同士で足したほうが早く計算できると思います。あとは子供の好みですかね。
長くなったので、小学生コースは次回に。
え~(・c_・`)
ウソです。ありがとうございます。楽しみにしています。小2ですけど、これもやってみようかな。
記号を使う力作なので、ゆっくり書いてください(^-^)/
草カゲさまの四角わけパズルを始めました。九九に効きそうですよ~。
こんにちは。
とりいれるのはやい!流石!
サイパーのはしてないんですが、某ピ幼児家庭教材にあったので結構やりましたよ。
7×7はまだ楽しいんですよ、13×13マスになるとね、もう見ている親も頭がウニ〜ですよ。
でも楽しいからがんばってー。
こんにちは。
二投目いきますよ。
今回は繰り上がりのある足し算小学生コースです。
今回は、水道方式のタイルの代わりに折り紙を使ったタイルもどきを作って使います。また、折り紙と同サイズの10×10マス目を紙に書いておきます。15cm四方の折り紙なら、1マス1.5cm四方、全体で15cm四方のマス目ですね。
タイルもどきに使う折り紙は全て同じ色にします。切る前に工作用紙など厚紙を貼っておくと、折れたりズレたりが減ります。
折り紙1枚から10本の短冊をつくり、1本の短冊を10等分して10個の正方形を作ります。また、1本の短冊を半分にして、5の短冊を作っておくと便利でしょう。折り紙3枚で、100の折り紙1枚、10の短冊12本、5の短冊10本、1の正方形30個作れます。
準備ができたらGO!
1)まずは数が認識できているか確認。
6〜9は、上に空きのマス目があるので、タイルの数だけでなく、10にいくつ足りないか意識した声かけもする。「10にあと2足りないから、これは8だね〜」でも「8はあと2で10になるね〜」でも。
5以下は、小学生なら数えなくても視認で判断できるはず。できなければ、何個かのおはじきを見せてすぐ隠す→子供が数を答える、といった遊びも試してみる。
□□□□
□□□□
■□□□
■□□□
■□□□
■□□□
■□■□
■□■□
■□■□
■□■□
8 4
2)繰り上がりのない足し算は、足される数に積み上げていきます。1+7と7+1のように、足される数とたす数が入れ替わっても答えは同じである、ということを見せて納得したら、1+7の時も足す数の7に1を加えるようにします。
3)繰り上がりのある足し算です。8+5の場合、1年生では5をさくらんぼで2と3にわけて8+2+3としてから答えをだしますが、タイルもどきを使う場合、8を10にするために足りない2を5からとってきて10にして、残った3とあわせれば答えが出ます。常に意識するのは「10に足りない数」なので、計算の速さと正確性はさくらんぼを使うより上だと思います。
□□□□
□□□□
■<10になりたいよー!
■□□□
■□□□
■□●<いくぞ!
■□●<おk!
■□●<いってら〜
■□●<tら〜
■□●<ら〜
↓
●□□□<8+5は13!
●□□□
■□□□
■□□□
■□□□
■□□□
■□□□
■●□□
■●□□
■●□□
4)二桁+一桁の足し算。ようやく10の短冊の出番です。23+8の場合、23は30まで7足りないので、8から7取ってきて30にし、残った1と合わせれば答えがでますね。計算だけなら、20+3+8にして、20+11で答えを出してもいいですが、二桁の数の一の位を繰り上げたほうが、計算速度は上です。
■■□□□□
■■□□□□
■■□□●<7人でいくぜ!
■■□□●<おう!
■■□□●<おk
■■□□●<いこー
■■□□●<いくいく〜
■■■□●<ちょまt
■■■□●<いくぞ〜
■■■□●<いってら〜
↓
■■●□□□
■■●□□□
■■●□□□
■■●□□□
■■●□□□
■■●□□□
■■●□□□
■■■□□□
■■■□□□
■■■●□□<23+8は31!
5)二桁同士の足し算を暗算で、の前に20+30のように一の位が0の数の計算。下のように10の短冊を置いたら、30を20の隣にずらす。教科書で鉛筆10本の束をいくつでン十!とやってますが、きちんと量で示したほうが理解がしやすいと思います。
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
■■□□■■■
6)二桁同士の暗算はこれまでの取り組みのまとめなので、文章での説明になります。5)でやった十の位の足し算(10の短冊の移動)のあと、一の位同士の足し算を行います。タイルで念入りに見せてあげてください。
計算式の場合、一の位から計算する筆算とは逆順になるのですが、慣れると楽だし速いです。一の位同士を足したら繰り上がりそうだな、という場合は、十の位の足し算の時に合わせてしまいます。86+45のような場合でも、80+40は120だけど6+5は10を超えるから130にしてしまって、あとで130に1を足す、という感じ。
二年生で習う筆算は、桁が大きくなってもやってることは一桁同士の足し算ですから、数量感覚が十分でなくても解けます。数量感覚に不安があるからこそ、100の折り紙、10の短冊、1の正方形などで繰り返し見せることが有効だと思います。怒らず焦らず吸水性の悪いスポンジでも、記憶に刷り込み刷り込み。
今日はここまで。ペンギン親子の健闘を祈ります
ぶたのこさん コメントありがとうございます。
懐かしい!
うちはもう末っ子が5年です。
1年生のさんすうでの第一関門はさくらんぼ。
これは賛否両論ですが、うちは、子供達が理解した方がいいと言ってました。
計算は学年が上がるほど、ぱっとみて覚えているので答えが出てしまうようになりますが、
1・2年生はぶたのこさんが書かれているように、数量感覚が微妙な子は必ずやっておいた方がいいかなと。
暗記しちゃう子もいるかもしれませんが、数量感覚は必ず身に着けておいてほしいです。
こんなの簡単じゃーんってバカにしていると、本当、痛い目にあいますので。
子供達が大きくなり、色々と分かることもあります。
サイトで書いてあるようなことは、面と向かっては言えません。
ここを訪れた方は何かのご縁。頑張ってほしいと思います。
管理人様、こんにちは。
息子が習ってきて初めてしったさくらんぼ計算ですが、繰り上がりの足し算の導入時期には分かり易い指導法だな、と感じました。1学期にしつこく繰り返した「いくつといくつ」がここで生きてきた!と感心したもんです。
我が家は先取りしていたのでさくらんぼの効果は分かりませんが、さくらんぼ計算で繰り上がり繰り下がりの計算を理解出来た子供も少なからずいるのだろう、と思います。10の補数で直接計算する方法に、補数を得て数の分解をする手順を加えるだけでさくらんぼ計算になるわけですから。
親世代が学んだ10の補数は、計算は早く正確にできますが、一桁同士だと丸暗記も出来てしまう程度なので本当に理解出来ているか分かりにくいんですよね。さくらんぼが入ることで、やるべき計算がわかりやすくなったのかな、と。でも結局、数量感覚に乏しくても計算できてしまうため、学年が上がるごとに落ちていく子供は減らないだろうとも思いますが。
足し算引き算掛け算割り算小数分数と、数量感覚は小学生の間ずっと必要です。ゆくゆくはさくらんぼなしで計算するくらいの数量感覚に鍛えるために、具体物の活用をもっと!(⁎⁍̴̆Ɛ⁍̴̆⁎)
こんにちは。
3投目の今日はようやくかけ算です。用意するタイルの種類も増えるので、タイルもどき作成用折り紙の色に気をつけてください。
用意するものは、2投目と同じサイズの10×10のマス目。15cm×15cmの折り紙を使うなら、15cm×15cmで外枠を作ってください。また、2投目で作った10と5の短冊、1の正方形も使います。その他、2、3、4、6、7、8、9の短冊を10本ほど作成して準備完了です。
なお、某ピ教育では、かけ算九九は覚えません。謎の10の段、1の段を経て、5の段は10の段の半分、2の段はかける数を二つ足す、ナドナド、足し算や引き算を駆使します。詳しく説明すると管理人様に迷惑がかかるかと思うので、九九の暗唱前提で説明していきたいと思います。
1)謎の10の段と1の段は、一番わかりやすいかけ算ですね。もう置き方の説明もいらないくらい。
10の段なら、マス目の左から順に10の短冊を1本置き「10かける1は?」→「10!」、二本目を置き「10かける2は?→「20!」てな感じです。最後に「10かける10は?」→「100!」
1の段は、マス目の左下から順に1の正方形をひとつずつ置いていきます。「1かける1は?」→「1!」、「1かける2は?」→「2!」
親子とも楽勝ですね。
2)2の段は、かける数が1増える毎に増える数も小さいのですぐに覚えられますね。2の短冊を九九を唱えながらかける数だけ並べていき、タイルの数と答えをしっかり結びつけてください。(例2×7のあたり)
また、かけられる数とかける数を入れ替えても答えは同じになる、ということを、タイルで数パターン見せて理解させてください。(例7×2のあたり)
□□□□□□□□□□
□□□□□□□□□□
□□□□□□□□□□
□□□□□□□□■■
□□□□□□□□■■
□□□□□□□□■■←7×2
□□□□□□□□■■
□□□□□□□□■■
■■■■■■■□■■
■■■■■■■□■■
↑2×7
3)5の段も、一の位が5と0の繰り返しなので、覚えるのは簡単ですね。
5の段で気にしたいのは、80の半分、50の半分など「10の段の半分」がわかっているかどうかです。40や80の半分は答えられても、50や70の半分が答えられなければ、10の短冊を並べて全て半分で切り離して結果を見せてください。数量感覚が微妙だと正しく答えられないようなので、確実にわかるようにインパクト重視で切っちゃいましょう。他の段と同じように九九を唱えながら5の短冊を置いていくのはその後で。
4)他の段も、九九を唱えながら短冊を置いていってください。九九の答えが合っているかどうか、視覚で確認しながら覚えていきます。特に大きい数同士のかけ算の場合は間違えやすいので、「かける数が1増えるとかけられる数の分だけ増えていく」というかけ算の特性を、タイルを使って丁寧に計算し覚えさせます。
ちなみに某ピ式だと9の段=10の段ー1の段、8=10−2、7=5+2、6=5+1、4=3+1=2+2=5−1、3=2+1で足し算と引き算を使って計算します。
5)かけ算を覚え始めた時、「10×□」は答えられるのに、なぜか「□×10」の答えに詰まる場合があるようです。九九にないから答えられない、ではなくて、かけ算は「かける数とかけられる数が逆になっても答えは同じ」なので、タイルで1回示せば大丈夫なはずです。
6)九九から飛び出て、11×11のような場合は、タイルでどうするか。
○○○○○○○○○○●
■■■■■■■■■■○
■■■■■■■■■■○ ■の範囲は100の正方形1枚=100
■■■■■■■■■■○ ○は10の短冊が2本=20
■■■■■■■■■■○ ●は1の正方形が1個=1
■■■■■■■■■■○ よって答えは、121
■■■■■■■■■■○
■■■■■■■■■■○
■■■■■■■■■■○
■■■■■■■■■■○
■■■■■■■■■■○
では13×7は?
○○○○○○○
○○○○○○○
○○○○○○○
■■■■■■■□□□
■■■■■■■□□□ ○は3×7=21
■■■■■■■□□□ ■は10×7=70
■■■■■■■□□□ ※□は空き
■■■■■■■□□□ 13×7の答えは、91
■■■■■■■□□□
■■■■■■■□□□
■■■■■■■□□□
■■■■■■■□□□
■■■■■■■□□□
今日はこの辺で。
ぶたのこさん 掛け算もありがとうございます。
学校でも授業でぶたのこさんが説明されたようなことを絶対にやってるはずなんですよ。
地域性もあるかもしれませんが、うちだと掛け算は多くの家庭で先取りしてそうな気がします。
低学年ですから、親も掛け算は覚えさせなきゃって暗記させるんです。
学校も実際は掛け算カードで、暗記させますから。
で、どうなるかっていうと、ぶたのこさんが書かれている数量感覚を教えても、「まどろっこしい。もう覚えてるもん」で終了。
暗記してない子も、皆がぱっと言えるから暗記しようとします。
駄目ですよね。
数量感覚が身についていることが前提で暗記なんです。
一番上はあんな感じなので、確認はしませんでしたが、下の2人は気になったので確認しました。
2人とも分かってましたが、これから掛け算を習う小2の子達は絶対に確認した方がいいです。
算数の数量感覚ってこんなところから始まってます。
今日は愚息から、数Ⅲの複素数平面の講座を受けました。
もうお腹いっぱいです。
管理人様、こんにちは。
複素数平面の聴講お疲れ様でした。ご長男は、ほんと数学が楽しいんですね。お腹いっぱいといいながらも、毎回付き合う管理人様の優しさがステキです。
九九は、特徴的な言い回しもあって小二で覚えるのは少々難しいため、丸暗記になるのは仕方ないのかもしれません。でも、先取りなら教える時に、または習った後すぐに暗記の手助けとしてタイルを用いた復習を家庭でもできたなら、低学年から塾に放り込まなくてもいいんですよね。でもやらないから子供は丸暗記でフエ〜ルワケワカメ(*´꒳`*)
ぶたのこさま
ありがとうございました。
3)は盲点でした。6)も面白いです。
算数の下巻の教科書をちら見してみましたが、各段ごとに文章題を挟むみたいです。
昔は一気に覚えてたように思うのですが。
校庭ペンギン様、こんにちは。
昨日図書館にいったら、ほねほねザウルスが5冊も置いてあったので全部借りて帰ったら、息子は帰宅後シャワーの後、ノーパンで読み始めましたよ。服着て?
教科書は各段ごとに文章題ですか、多分親世代からそうなんじゃないかな〜と思うんですけど、昔すぎて自信がありません。十年ひと昔とはいいますが、ひと昔ふた昔どころじゃないからね…。
3)については「10の半分は5なんだから、わかるでしょ?」と思うんですけど、十の位が奇数の時は十単位で等しく分けられなくて困るようです。九九とはあまり関係ありませんが、思考の幅を広げるため、ここだけ某ピ式を残してみました。
6)は、筆算を習う前でもタイルで計算できるので、九九を覚えた後にでも見せてあげるといいかもしれません。13×7は、5×7+8×7で計算してもいいですし、6×7+7×7だって答えは同じですし。
学校で習ったことよりも少し先を知ることで、今習っていることの理解が進むのではないかと考えています。かけ算をタイルであらわす意味も、面積を習い始めてようやく気づくのかもしれません。低学年の子は目先のことしか眼中にないので、親が意識して少し先を示す必要があると思います。
おおっと、語っちまった。
かけ算(特に先取りの場合)の数量的感覚と原理原則を理解できるようにつくられている問題集でこぐま会のひとりでとっくんかけ算(1)(2)を今の時期のタイミングでやる事をおススメします
サイパーの四角分けパズルとあわせてやっていくといいのかなと思いました
数量感覚を意識して進めるかけ算ドリルは多くないのでひとりでとっくんシリーズのかけ算はとてもおススメです
九九算を学校で習う前にかけ算として理解してもらいたくて先取りして取り組んでいましたよ
結果的にかけ算、わり算のひっ算、小数の四則計算と先取りしていってしまいました(ついでという感覚で進めていった結果です)
分数の四則計算も同様です
分数はかけ算、わり算、たし算、ひき算の順で進めていく事をおススメします(学校で教わる順番と違いますが、躓きにくい順番になるのでおススメです)
算数の探険シリーズのたすひくかけるわるもおススメです
高い本なので図書館で借りて使われる事をおススメします
数量感覚を理解しながら仕組みがわかるお話形式で進む内容になっています
問題の計算が難しいのである程度計算力がついてから問題にチャレンジしてみてくださいね
草カゲ様、こんにちは。
こぐま会のひとりでとっくんシリーズの小学生版は、隠れた(?)名作ですよね。こぐま会の数分野は水道方式を参考にしているはずなので、ドリルを選ぶならこぐま会、でしょうか。実店舗での取り扱い書店は限られていますが、ネットでも買えるので問題ないかな。
でもなんだかすぐに品切れの予感が!
こぐま会は小学受験で有名な教材なんですよね(幼児向け教材はとっても沢山ありました)
小学生向けはひっそりと知る人ぞ知る問題集だと思うのです(ハイ、水道方式です)
実店舗で扱っているところがサイパーもそうなんですが、少ないんですよね
でも、単元毎に分かれていて痒いところに手が届くタイプの問題集で好きでした
3年生で終わってしまうのが残念な問題集です
面積図でかけ算と割り算を教えられれば受験算数がスムーズに進みますよ
以外なところで面積図が出てくると、エッ!
算数って奥深くって面白いなぁと思うような解説をあちらこちらで見かけて1人興奮しております(子供は、はい、はいわかった、わかったと冷たい視線が…)
こんにちは。
4投目はわり算です。
かけ算九九の暗唱ができて、ドリルなどでも各段間違えずに答えを書き、かけられる数かかける数のどちらかが□になっているような問題も解けるようになっていれば、わり算の計算は問題ないでしょう。ただ、問題なのは文章題で、同じ「12÷3」と式を立てる場合でも、計算が合っていても助数詞(個や人など)を間違えると×になるので、わり算での必要な二種類の考え方を理解させるためにタイルを用います。
1)かけ算の文章題は、「かけられる数(1あたりの数)×かける数(いくつ分)=積(全体の数)」ですから、文章から(1あたりの数)と(いくつ分)を探し、書く順に気をつけて式を立てます。(1あたりの数)と(いくつ分)を逆に書くと×ですよ。タイルで表せば、縦「かけられる数(1あたりの数)」、横「かける数(いくつ分)」です。足し算引き算の時と違い、助数詞が複数でてくるので、助数詞も間違えないように。
↑□□□□□□□□□□
か□□□□□□□□□□
け□□□□□□□□□□
ら□□□□□□□□□□
れ■■■■□□□□□□例)3個×4人=12個
る■■■■□□□□□□
数■■■■□□□□□□
→かける数(いくつ分)
2)わり算の計算式は「(全体の数)÷わる数」で表されますが、(わる数)がかけ算の(1あたりの数)と(いくつ分)のどちらになるかによって答えの意味が異なります。
①「(全体の数)÷わる数(いくつ分)=商(1あたりの数)+余り
②「(全体の数)÷わる数(1あたりの数)=商(いくつ分)+余り
例えば、シャインマスカット24粒を家族4人で分けたら一人何粒になるかが①、シャインマスカット24粒を一人4粒で分けたら何人に分けられるかが②で、式と答えは同じ「24÷4=6」でも、助数詞を含めた答えは①「6粒」、②「6人」と異なります。
このあたりは生活の中で経験できることですが、経験がないと違いがわからず、わり算の計算はできても問題文の理解ができずにつまずく原因になるので、機会があれば子供に盛り付けのお手伝いなどをさせましょう。
3)『①「(全体の数)÷わる数(いくつ分)=商(1あたりの数)+余り』のタイルの置き方です。からあげ12個を3人で分ける場合、おはじき12個のうち、まず横に3個置き(1回目)、上のマスに3個置き(2回目)、また上に3個(3回目)…と3個ずつ繰り返し置いていきます。配ると全員が同じ数にならないおはじきが残ったら余として隣に並べます。この場合4回目まで同じ数で配れたので、4個が答えです。
□□□□□□□□□□
ひふさ□□□□□□□ 12個÷3人=4個
とたん□□□□□□□
りりに□□□□□□□
□□ん□□□□□□□
□□□□□□□□□□
●●●□□□□□□□←4回目
●●●□□□□□□□←3回目
●●●□□□□□□□←2回目
●●●余□□□□□□←1回目
4)『②「(全体の数)÷わる数(1あたりの数)=商(いくつ分)+余り』の置き方です。例えばドーナツ12個をひとりに3個ずつ分ける場合として、まずひとり分3個のおはじきを縦に並べて置きます。おはじきが無くなるまで隣に3個ずつ置いていき、余りは隣に並べます。おはじきが縦に3個並んだ列の数(4人)が答えです。
□□□□□□□□□□
ひふさよ□□□□□□ 12個÷3個=4人
とたんに□□□□□□
りりにん□□□□□□
ぶぶんぶ□□□□□□
んんぶん□□□□□□
□□ん□□□□□□□
●●●●□□□□□□
●●●●□□□□□□
●●●●余□□□□□
推敲してないけど、今日はここまで。次で最後?
久しぶりに投函です。4年生になってもーたけど、小数と分数のかけ算いきます。
小数も分数も、かけ算は面積で考えると便利です。図形で面積を習っていなくても、かけ算九九で使ったタイルもどきを利用すれば多分大丈夫だと思います。
1)小数のかけ算(0.2×0.7の場合)
□□□□□□□□□□
□□□□□□□□□□ 全体を縦1×横1で「1」とする。
□□□□□□□□□□ □と■はそれぞれ縦0.1横0.1で、
□□□□□□□□□□ □と■の一つの量は0.01。
□□□□□□□□□□ 全体量「1」が100等分になっているので
□□□□□□□□□□ 1/100=0.01。
□□□□□□□□□□
□□□□□□□□□□ 見た目は2×7だけど、■一つは0.01だから
■■■■■■■□□□ 答えは0.14。
■■■■■■■□□□ 0.2×0.7=0.14
2)分数のかけ算(1/2×1/7)
折り紙一枚を折ったり切ったりしながら、量が減っていくところを見せます。
最後の答え部分を塗ったり、切り離したものを寄せて全体量「1」を作り、子どもが全体量「1」のうちどれだけの量が残ったか、一目見てわかるように工夫を。
「分子×分子/分母×分母」は、できればこどもに発見させる。
□□□□□□□ まず、折り紙を半分(1/2)に折ります。
■■■■■■■ (■部分)
↓
□□□□□□□ 次に、横1を1/7にします。
■□□□□□□
全体量「1」が14等分されたうちの一つなので、1/14が答え。
3)分数のかけざん(3/4×5/7)
□□□□□□□ やり方は2)と同じで。
■■■■■■■
■■■■■■■
■■■■■■■
↓
□□□□□□□
■■■■■□□
■■■■■□□
■■■■■□□
全体量「1」が28等分されたうちの15が残ったので、15/28が答え。
「分子×分子/分母×分母」は、できればこどもに発見させる。
ぶたのこさん コメントありがとうございます。
最初のくだりに笑ってしまいましたが大事よ。
数量感覚は絶対に身につけないといけません。
絶対なんです。
この図、懐かしい。
ぶたのこさんともお付き合いはもう2年?になりますか。
このご縁に感謝です。